Physics 9 Solved Paper 2018 Overseas Federal Board
Class 9 Physics Solved Paper 2018 Overseas
Class 9 Physics Solved Paper 2018 Overseas for Federal Board is available in this post. You can see more FBISE solved past papers of class 9 on our website.
Class 9 Physics Solved Paper 2018 Overseas
Section A
Q1. MCQs
Class 9 Physics Solved Paper 2018 Overseas
Section B
Q2.
(i) On closing the jaws of a Vernier Callipers, zero of the Vernier Scale is on the left to its main scale zero such that the 4th division of its Vernier Scale coincides with one of the main scale divisions. Find its zero error and zero correction.
Sol: On closing the jaws of a Vernier Callipers:
Main scale reading = – 0.1 cm
Vernier division coinciding with main scale = 4th div
Vernier scale reading = 4 x 0.01 cm = 0.04 cm
Zero error of the Vernier Callipers = (- 0.1 + 0.04) cm = – 0.06 cm
Zero Correction of the Vernier Callipers = + 0.06 cm
(ii) Name any six base quantities.
Ans. The names of six base quantities are:
1. Length (l)
2. Mass (m)
3. Time (t)
4. Electric current (I)
5. Intensity of light (L)
6. Temperature (T)
(iii) Why is the value of ‘g’ taken as negative when a body is thrown vertically upwards?
Ans. When a body is thrown vertically upwards, its velocity is decreasing due to the force of gravity acting on it, so the acceleration due to gravity (g) is taken as negative i.e. g = – 10 ms–2.
(iv) Find the acceleration of a body if it is moving with uniform velocity?
Ans. The acceleration of a body is the rate of change of its velocity. For a body moving with uniform velocity, there is no change in the velocity of the body. Hence, its acceleration will be ZERO.
(v) State Newton’s second law of motion.
Ans. Newton’s Second Law of Motion
This law states that “When a net force acts on a body, it produces acceleration in the body in the direction of the net force. The magnitude of this acceleration is directly proportional to the net force acting on the body and inversely proportional to its mass”.
(vi) A stone attached to a 1m long string is moving with a speed of 5ms-1 in a circle. Find the centripetal acceleration of the stone.
Sol. Radius of circle = r = 1m
Speed = v = 5 ms-1
Centripetal acceleration = ac =?
Using formula
ac = v2 / r
ac = (5)2 / 1
ac = 25 ms-2
(vii) Why a body can not be in equilibrium under the action of a single force?
Ans. In the case of a single force, the net force is not zero so acceleration is produced. Therefore, under the action of a single force, a body can not be in equilibrium.
(viii) On what factors the orbital speed of a satellite depends?
Ans: The formula of orbital speed is:
vo = √gh (R + h)
The above formula shows that the orbital speed of a satellite depends upon g, R, and h. Since R and g both are constant, therefore, the orbital speed of the satellite depends on h (its altitude above Earth).
(ix) Define work. Give its two formulas and SI-Unit.
Sol. WORK
Work is said to be done when a force acts on a body and moves it through some distance in the direction of the force. Work is therefore equal to the product of force and distance. It is given by
Work done = Force x displacement
W = FS
Sometimes the force makes an angle ‘θ’ with the direction of motion, then the work done is given by:
W = (F Cosθ) S
Where F Cosθ is the components of force along which the body moves and covers the distance S.
UNIT OF WORK
The SI unit of work is ‘Joule’.
(x) At sea level, the atmospheric pressure is about 0.01013kNcm-2. Convert it into Nm-2.
Excluded from Syllabus for Annual Exam 2021
(xi) Define specific heat and give its formula.
Ans. Specific Heat
Specific heat of a substance is the amount of heat required to raise the temperature of 1 kg of that substance by 1 K (Kelvin). It is denoted by ‘c’. Its unit is Jkg-1K-1. Mathematically, it is given by:
C = ∆Q / (m ∆T)
We can find the specific heat of a solid by using the above formula.
(xii) How does hot tea remain hot for a long time in a thermos flask?
Excluded from Syllabus for Annual Exam 2021
(xiii) Define conduction and convection of heat.
Ans. Conduction of Heat:
The mode of transfer of heat by vibrating atoms and free electrons in solids from hot to cold parts of a body is called the conduction of heat.
Convection of Heat:
Transfer of heat by actual movement of molecules from a hot place to a cold place is known as convection of heat.
(xiv) A machine is 12% efficient. If useful work done by the machine is 6 joules then calculate the total energy consumed by the machine.

(xv) What is the purpose of constriction in a clinical thermometer?
Ans. The purpose of constriction in a clinical thermometer is to prevent the mercury to return. Thus, its reading does not change until reset.
Class 9 Physics Solved Paper 2019 Overseas
Section C
Q3. a. Define and give two examples of each:
i. Pre-fixes (2)
ii. Vibratory motion (2)
iii. Third law of motion (2)
Ans. i. Prefixes:
The words or letters added before a unit and stand for the multiples or submultiples of that unit are known as prefixes.
Example:
Kilo (k) and Mega (M) etc.
ii. Vibratory motion
To and fro motion of a body about its mean position is known as vibratory motion.
Example:
The motion of a child and a swing.
iii. Third Law of Motion
To every action, there is always an equal but opposite reaction.
Example:
Motion of rocket
Q3. b. Find the magnitude and direction of a force if its x-component is 12N and y-component is 5N. (2+2)
Sol. Horizontal Component = Fx = 12N
Vertical Component = Fy = 5N
Magnitude of force = F =?
Direction of force = θ =?
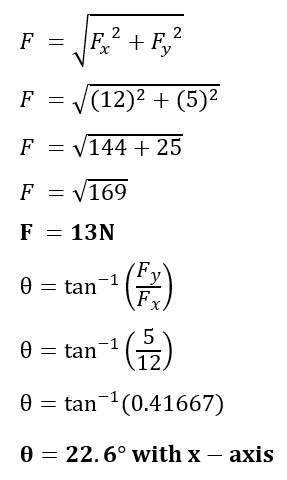
Q4. a. Define equilibrium and explain the first condition for equilibrium. (1+2)
Ans. Equilibrium
A body is said to be in equilibrium if no net force acts on it.
Examples
A book lying on a table or a picture hanging on a wall.
First Condition for Equilibrium
According to this condition, a body is said to be in equilibrium if the sum of all the forces acting along any straight line on a body is zero.
Let ‘n’ number of forces F1, F2, F3,.…,Fn are acting on a body such that
F1+F2+F3………….+Fn = 0
or ƩF= 0
or ƩFx = 0 and ƩFy = 0
Then the body is said to satisfy the first condition of equilibrium.
Q4. b. The acceleration due to gravity on the surface of the moon is 1.62 ms-2 and the radius of the moon is 1740km. Find the mass of the moon. (4)

Q4. c. Write a note on Kelvin scale of temperature. (3)
Ans. Kelvin Scale of Temperature: In SI units, the unit of temperature is Kelvin (K) and its scale is called the Kelvin scale of temperature. The interval between the lower and upper fixed points is divided into 100 equal parts. Thus, a change in 1°C is equal to a change of 1K. The lower fixed point on this scale corresponds to 273 K and the upper fixed point is referred to as 373 K. The zero on this scale is called the absolute zero and is equal to – 273 °C.
Q5. a. How does Archimedes Principle help to determine the density of an object? (4)
Ans: Density of an Object
According to the Archimedes principle, the ratio between the weight of an object and the weight of an equal volume of liquid is the same as the ratio in their densities. Therefore, the density of an object can be determined by the following method.
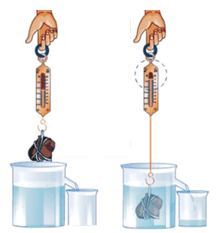
Let the density of object = D
The density of the liquid = ρ
Weight of object in Air = w1
Weight of object in liquid = w2
Weight of an equal volume of liquid w = w1 – w2
As D / ρ = w1 / w
or D = w1 / (w1 – w2) x ρ (Where w = w1 – w2)
Q5. b. Define latent heat of fusion. Also, give its formula. (2+1)
Ans. Latent Heat of Fusion: Heat energy required to change the unit mass of a substance from solid to liquid state at its melting point without change in its temperature is called its latent heat of fusion.
It is denoted by Hf
Hf = ΔQf /m
ΔQf = m Hf
Q5. c. How does a greenhouse trap solar energy? (3)
Ans. Light from the Sun contains thermal radiations (infrared) of long wavelengths as well as light and ultraviolet radiations of short wavelengths. Glass and transparent polythene sheets allow radiations of short wavelengths to pass through easily but not long wavelengths of thermal radiations. Thus, a greenhouse becomes a heat trap. Radiations from the Sun pass easily through the glass and warms up the objects in a greenhouse. These objects and plants such as give out radiations of much longer wavelengths. Glass and transparent polythene sheets do not allow them to escape out easily and are reflected
back in the greenhouse.




