Physics 9 Solved Model Paper 2020 Federal Board

Class 9 Physics Solved Model Paper 2020

Class 9 Physics Solved Model Paper 2020 for Federal Board is available in this post. You can see more FBISE solved past papers of class 9 on our website.

Class 9 => ( Physics Notes | Model Papers | Past Papers | Solved Papers | Solved MCQs )

Class 9 Physics Solved Model Paper 2020

Section A

Q1. MCQs

Class 9 Physics Solved Model Paper 2020
Section B

Q2.

(i) Differentiate between axis of rotation and line of action of a force with the help of figure.

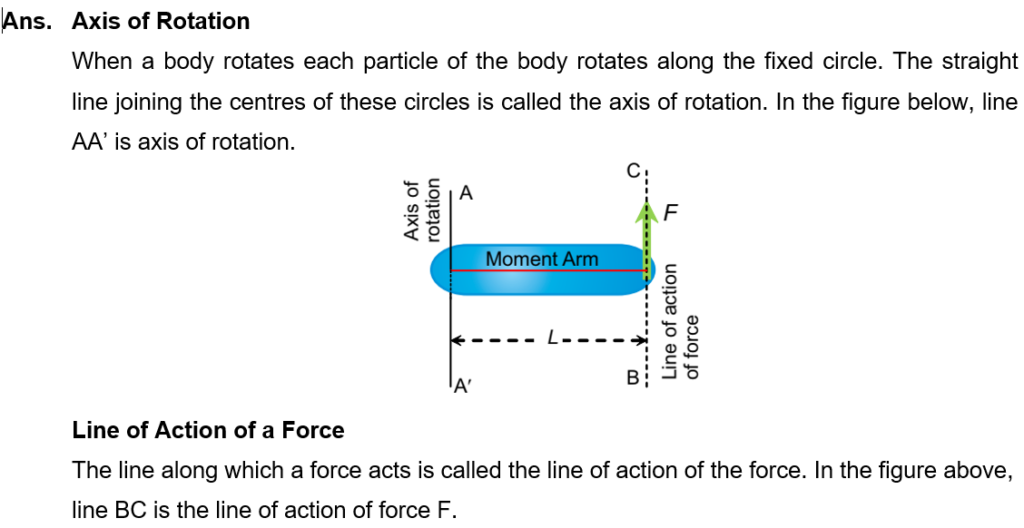
(ii) A pencil is just balanced at its tip, what is its state of equilibrium? Answer with reason.

Ans.  A pencil balanced at its tip is in unstable equilibrium because whenever we leave it, the pencil topples over about its tip and falls down.
In unstable equilibrium, a body may be made to stay only for a moment. Thus, a body is unable to keep itself in a state of unstable equilibrium.

(iii) Write three advantages and disadvantages of friction. (Definition of friction is not required)

Ans.    Advantages of Friction
1. Motion would not have been possible without friction. e.g. we cannot run on the slippery ground because it offers less friction. 
2. Friction is also necessary to stop a moving body.
3. A nail stays in the wood only because of friction.

Disadvantages of Friction
1. Friction produces heat in various parts of machines. Thus useful energy is wasted as heat and sound energy.
2. It causes wear and tear in different parts of machines.
3. Vehicles like cars, buses, and trains lose part of their energy in overcoming friction.

(iv) Speed of a train increases from 36 km/h to 72k m/h in 10 minutes. Find the distance covered by the train during this time.

(v) Describe the factors on which the accuracy of a measurement depends?

Ans. The accuracy in measuring a physical quantity depends upon various factors:
1. the quality of the measuring instrument
2. the skill of the observer
3. the number of observations made

(vi) Why is it assumed that a gravitational field exists all around the Earth?

Ans.  Since the gravitational force of attraction is present all around the earth therefore it is assumed that a gravitational field exists all around the earth.

(vii) For a body of Mass ‘m’ moving in a circle of radius t if its velocity is halved, what will be the effect on the value of centripetal force?

(viii) At what altitude the value of ‘g’ would become one fourth (1/4) of the surface of the earth?

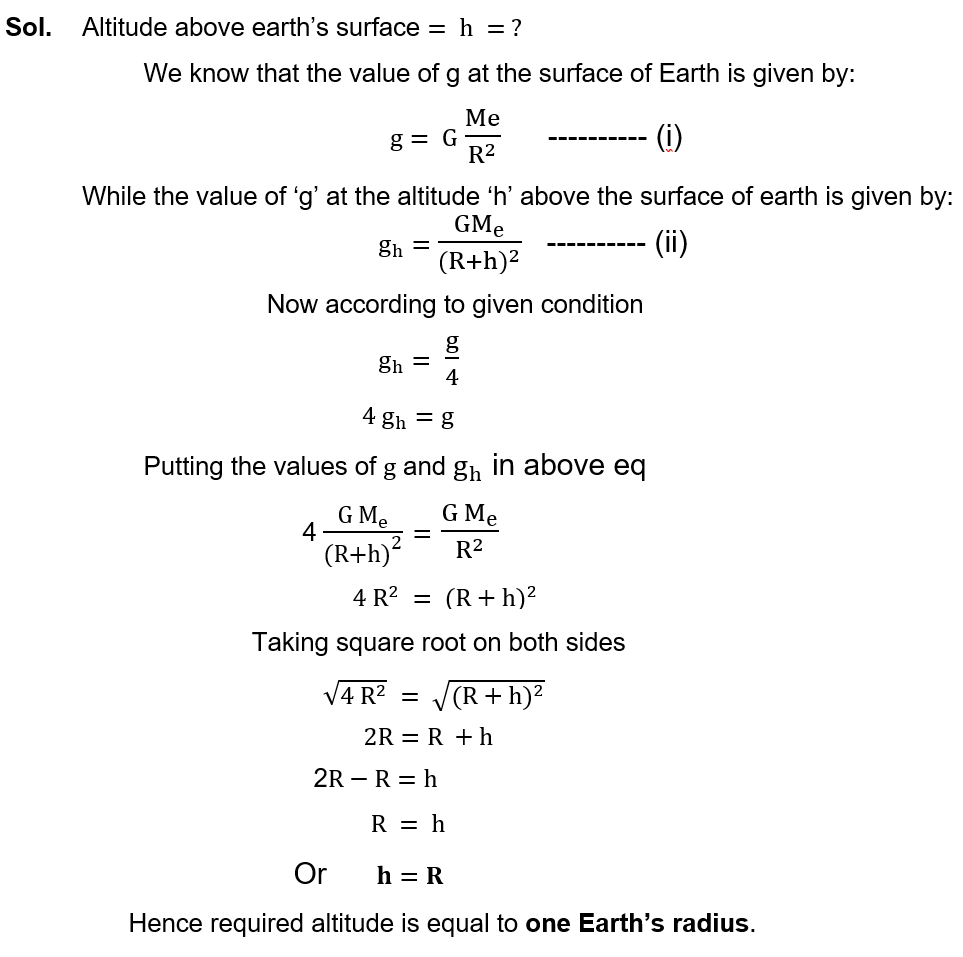
Class 9 Physics Solved Model Paper 2020
Section C

Q3.

(i) State the reason, why does a bimetallic strip bend on heating and/or cooling?

Ans. A bimetal strip consists of two thin strips of different metals such as brass and iron joined together. On heating the strip, brass expands more than iron. This unequal expansion causes bending of the strip.

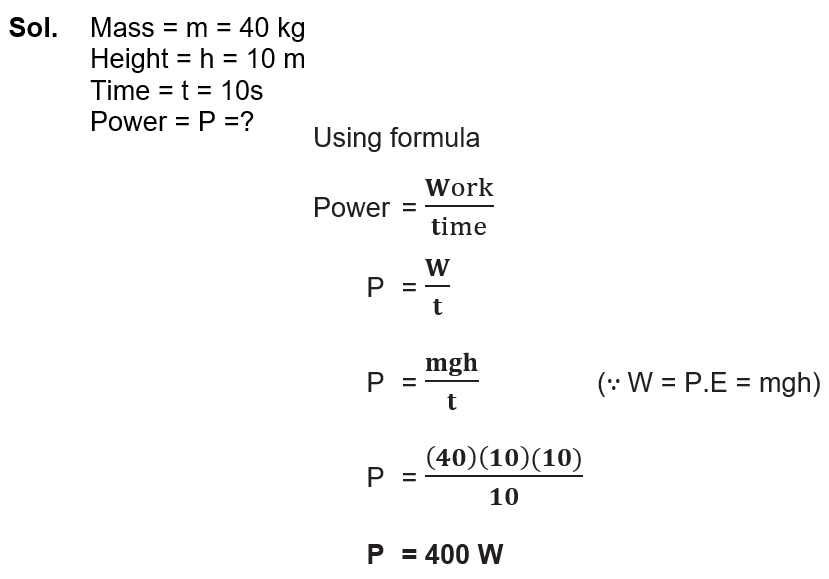
(ii) How much power is used by a 40 Kg athlete in climbing a 10m high ladder in 10s?

(iii) When a person takes a bucket to some distance, work done by him is zero, why?

Ans. In Physics, work is done when we apply a force on a body and it covers some distance in the direction of the force.
When a person takes a bucket to some distance, he applies a force in the vertical direction, but the bucket moves in the horizontal direction. Since the bucket does not cover any distance in the direction of force, therefore, work done in this case is zero.

(iv) How the effectiveness of a small force is increased when the action area of force is reduced?

Ans. The effectiveness of a small force is increased if the effective area of the force is reduced. For example, the area of the tip of the pencil or that of the nail is very small and hence increases the effectiveness of the force.

(v) Why do we feel cool after perspiration/sweating?

Ans. It takes energy to evaporate sweat off of our skin, and that energy is heat. As our excess body heat is used to convert beads of sweat into vapors, so we feel cool after perspiration/sweating.

(vi) Prove that K.E = ½ mv²

Ans. Derivation of  K.E = ½ mv²

Consider a body of mass ‘m’ moving with velocity ‘v’. The body stops after moving through some distance ‘S’ due to some opposing force such as the force of friction acting on it. The body possesses kinetic energy and is capable to do work against opposing force F until all of its kinetic energy is used up.
K.E. of the body = Work done by it due to motion
K.E = FS     …. (i) 
Here,  vi = v,   vf = 0
As F = ma
∴ a = (-F)/m    (Since motion is opposed, hence, ‘a’ is negative.)                                                           
Using the third equation of motion
2aS     =  vf² – vi²                                               
or  2(-F/m) S = (0)² – v²
 -2FS / m = – v²  
FS = ½ mv² …… (ii)
From eq (i) and eq (ii), we get  
K.E = ½ mv²

(vii) What are the factors on which the rate of flow of heat in solids depends?

Ans. The rate of flow of heat in solids depends on the following factors:
1. Cross-sectional area of the solid
2. Length of the solid
3. Temperature difference between the ends of the solid

Class 9 Physics Solved Model Paper 2020
Section D

Note: Attempt any TWO questions. All questions carry equal marks.

4.(a) Is there any absolute rest or motion? Describe the types of motion with one example for each type. (6)

Ans.  No, there is no absolute rest or motion. The state of rest or motion of a body is relative.
For example, a passenger sitting in a moving bus is at rest because he/she is not changing his/her position with respect to other passengers or objects in the bus. But to an observer outside the bus, the passengers and the objects inside the bus are in motion.

Types of Motion
There are three types of motion.
(i) Translatory motion (linear, random, and circular)
(ii) Rotatory motion
(iii) Vibratory motion (to and fro motion)           

Translatory motion
In translational motion, a body moves along a line without any rotation. The line may be straight or curved.
Examples:
1. Aeroplanes flying straight in the air.
2. The motion of gas molecules.

Rotatory motion
The spinning motion of a body about its axis is called its rotatory motion.
Examples:
1. The motion of a wheel about its axis.
2. The motion of the Earth about its geographic axis.

Vibratory motion
To and fro motion of a body about its mean position is known as vibratory motion.
Examples:
1. The motion of a child and a swing.
2. The motion of the pendulum of a clock.

4.(b) Recoil of a rifle is – 0.4 ms^-1 having a mass of 5 kg. What is the velocity of the bullet, if the mass of the bullet is 20 g?  (4)

Sol.     Mass of rifle = M = 5 kg
Recoil of rifle = V = – 0.4 ms^-1
Mass of the bullet = m = 20 g = 20/1000 = 0.02 kg
Velocity of the bullet = v =?
According to the law of conservation of momentum
MV + mv = 0
(5) (-0.4) + (0.02) v = 0
– 2 + 0.02 v = 0
0.02 v = 2
v = 2 / 0.02
v = 100 ms^-1
Thus, the velocity of the bullet will be 100 ms^-1.

5.(a) Derive an expression for the orbital speed of an artificial satellite, and also calculate the value of the orbital speed of a satellite close to the earth.  (5)

Ans. Consider a satellite of mass m revolving around the Earth at an altitude h in an orbit of radius r_o with orbital velocity v_o. The necessary centripetal force required is given by the equation:
F_c = mv_o² / r_o
This force is provided by the gravitational force of attraction between the Earth and the satellite and is equal to the weight of the satellite w (mg.). Thus
F_c = w’ = mg_h
or mg_h= mv_o² / r_o
or v_o² = g_h r_o
or v_o = √ g_h r_o
as r_o= R+h
v_o = √ g_h (R+h)
The above equation gives the velocity, that a satellite must possess when launched in an orbit of radius r_o = (R + h) around the Earth. An approximation can be made for a satellite revolving close to the Earth such that R >> h.
R+h = R
and g_h=g
∴ v_o =√g R
A satellite revolving around very close to the Earth has a speed v_o nearly 8 kms ^-1 or 29000 kmh^-1 .

5.(b) Describe and explain Hooke’s law graphically.     (5)

Ans. Hooke’s Law
This law states that within the elastic limit, the strain produced in a body is directly proportional to the stress applied to it. Mathematically,
Stress ∝ Strain
Stress = (Constant) x Strain
Stress/Strain = Constant

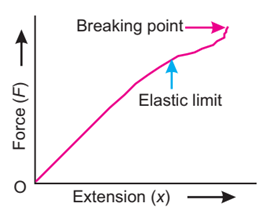
Hooke’s law is applicable to all kinds of deformation and all types of matter i.e., solids, liquids or gases within certain limits. This limit tells the maximum stress that can be safely applied on a body without causing permanent deformation in its length, volume or shape. In other words, it is a limit within which a body recovers its original length, volume or shape after the deforming force is removed. When stress crosses this limit, called the elastic limit, a body is permanently deformed and is unable to restore its original state after the stress is removed.

6.(a) Calculate the latent heat of fusion of ice experimentally. (The specific heat of water is 4200 JKg^-1K^-1). (6)

Ans: Experiment:
Take a beaker and place it over a stand. Put small pieces of ice in the beaker and suspend a thermometer in the beaker to measure the temperature. Place a burner under the beaker. The ice will start melting. The temperature of the mixture containing ice and water will not increase above 0°C until all the ice melts. Note the time that the ice takes to melt completely into the water at 0°C.

Continue heating the water at 0°C in the beaker. Its temperature will begin to increase. Note the time that the water in the beaker takes to reach its boiling point at 100°C from 0°C.

Draw a temperature-time graph as shown in the figure below.

Calculate the latent heat of fusion of ice from the data as follows:

Let the mass of ice = m

Finding the time from the graph:

Time taken by ice to melt completely at 0°C = t_f = t₂-t₁ =  3.6 min.

Time taken by water to heat from 0°C to 100°C = t_o = t₃-t₂ =  4.6 min.

Specific heat of water c  = 4200 Jkg^-1 K^-1 .

Increase in the temperature of water = Δ T = 100°C =100 K

Heat required by water from 0°C to 100°C = Δ Q = mc Δ T

=m × 4200 Jkg^-1 K^-1 × 100K

= m × 420 000 Jkg^-1

= m × 4.2 ×  Jkg^-1

Heat Δ Q is supplied to water in time to raise its temperature from 0°C to 100°C. Hence, the rate of absorbing heat by the water in the beaker is given by

Rate of absorbing heat = ΔQ / t_o

∴ Heat absorbed in time t_f = Δ Q_f = Δ Q × t_f / t_o

Since  ΔQ_f  =  m × H_f                   

Putting the values, we get

m × Hf   =  m × 4.2 × 10⁵ Jkg^-1  × t_f / t_o

or  Hf = 4.2 × 10⁵ Jkg^-1  × t_f / t_o

The values of t_f and t_o can be found from the graph. Put the values in the above equation to get

H_f = 4.2 × 10⁵ Jkg^-1  × 3.6 min / 4.6 min

H_f = 3.29× 10⁵ Jkg^-1

The latent heat of fusion of ice found by the above experiment is 3.29 × 10⁵ Jkg^-1 while its actual value is 3.36 × 10⁵ Jkg^-1.

6.(b) How much heat is lost in an hour through a glass window measuring 2.0 cm by 2.5 cm when the inside temperature is 298 K and that of the outside is 278K. The thickness of the glass is 0.8 cm and the value of K for glass is 0.8Wm^-1K^-1?   (4)

Solution:   Time = t = 1hour = 3600 s
Thickness of glass = L = 0.8 cm = 0.8/100 = 0.008 m                      
Area of a glass window = A = 2.0 m x 2.5 m = 5 m²
Temperature outside the house = T₁ = 298 K
Temperature inside the house = T₂ = 278 K

Change in temperature = ∆T = T₁ – T₂ = 298 – 278 = 20 K

Value of conductivity for concrete = k = 0.8 W m ^{– 1} K ^{– 1}

Rate of conduction of thermal energy = Q/t = ?

Q/t = kA (T1 – T2) / L

Q =  kA (T1 – T2) / L * t

Q / t = 0.8 * 5 * 20 / 0.008 * 3600 = 36,000,000 J = 3.6 x 10 ⁷ J